Functional Representation of Biofilm Growth
One of my current projects is a biofilm model that works on large-scale flow cells (large scale being on the order of millimeters). For example, I will be talking about a 2D simulation of the flow cell where the biofilm grows on the top and bottom of the chamber and the fluid inflow is on the left side and the outflow on the right. My model calculates the growth of the biofilm based on flow rate and concentration of nutrients. Originally, the growth would be directly up. However, if the biofilm has a curved surface, this approximation is not correct. It underestimates growth because it doesn’t take into account mass moving into a location from other sides. Instead, let \(h\) be the height of the biofilm and \(F\) be the speed of the interface. Then the equations for motion become: \(\frac{dh}{dt} = F\sqrt{1+\frac{dh}{dx}}\)
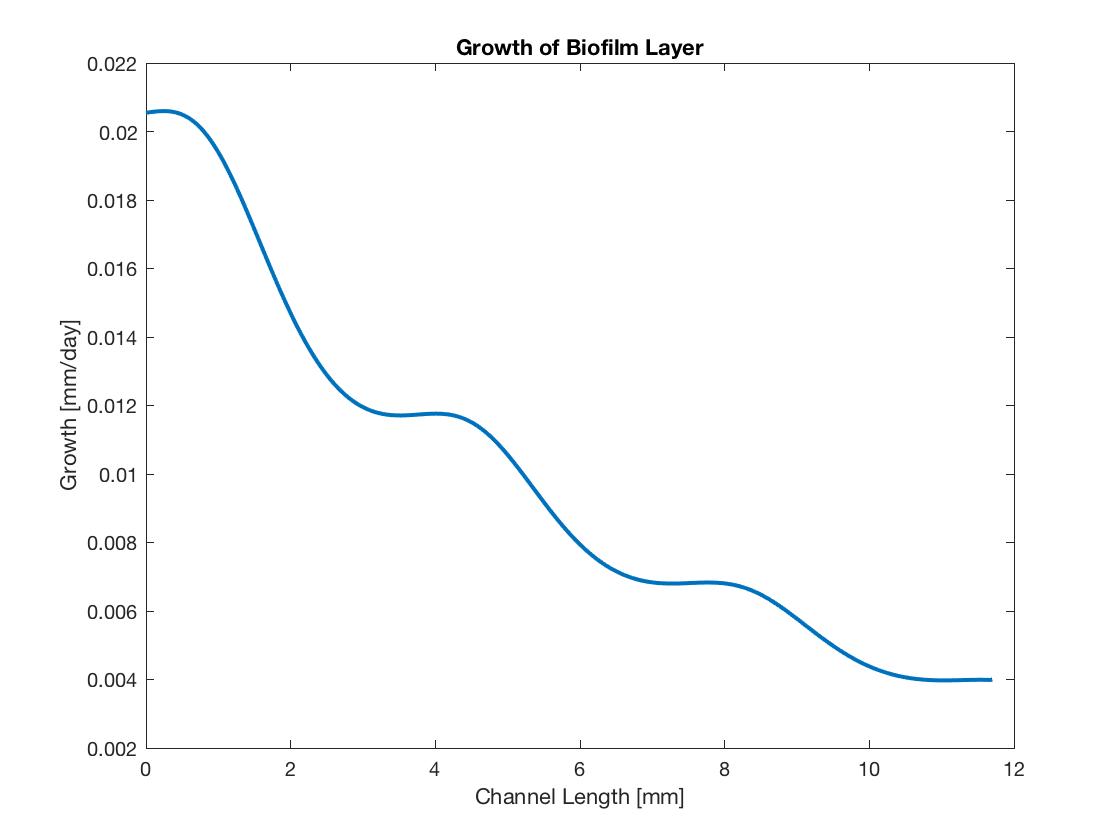
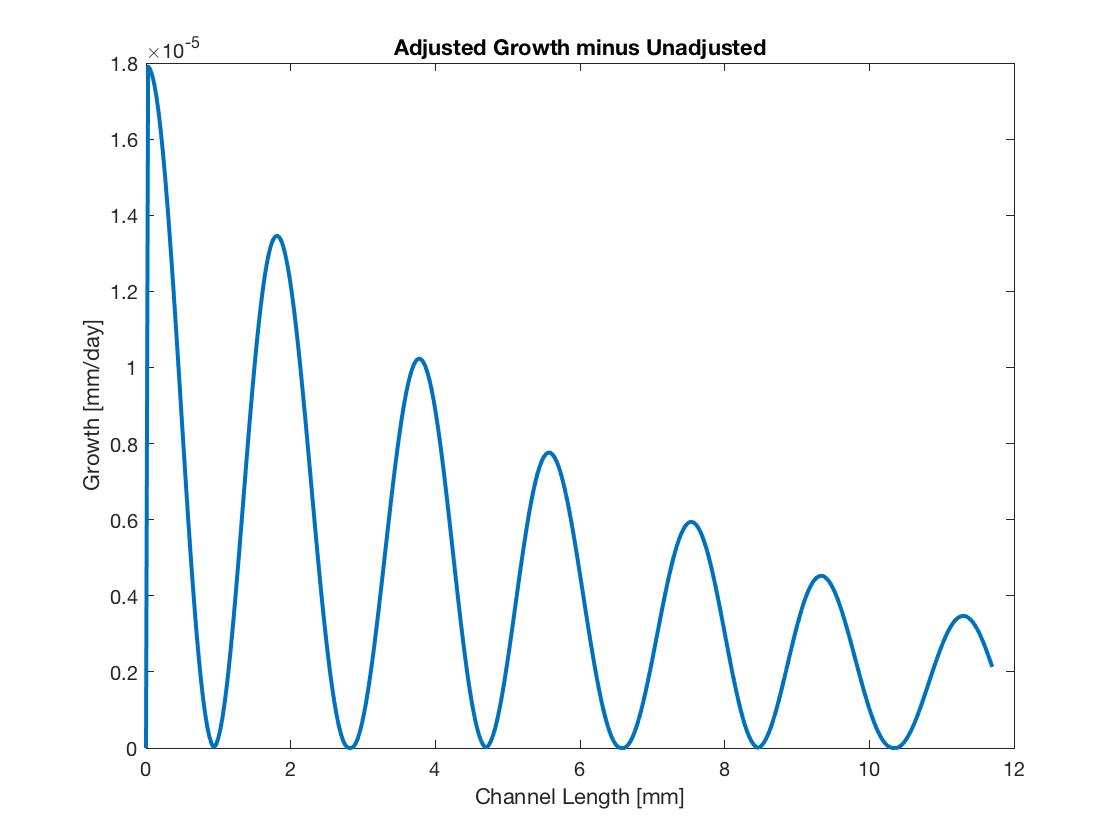
This gives us a functional representation for growth. Below is a plot for growth and a plot for the change in growth with this change to the equation. The height of the channel is 0.6 mm, and the height of the biofilm is .005 mm on average with sinusoidal surface with amplitude .0025 mm. We see that the growth is the same at the top and bottom of the sine shape, but at the steepest part of the surface, the adjusted growth is higher. Still this difference has only a small effect on the growth calculations (though for larger amplitudes the effects would be large).