Lateral Expansion of Biofilm
I made it back from SIAM Life Sciences in Minnesota after giving a successful talk! I got a few interesting questions, primarily about dealing with boundary layers for the substrate along the biofilm interface. After a nice vacation to Fort Lauderdale, I’m back to work.
I’m trying to finish asymptotic biofilm model that I presented at Life Sciences. One complication that I’m working on is adding the ability of biofilm to start in a clump at the middle of the flow cell and having the biofilm expand laterally to fill the plate. This is a difficult problem because in order for the biofilm to grow, there must be biomass there. So we need a way to allow biofilm to expand outward.
We would like to know what shape the biofilm would have so that it moves upward while keeping the same shape. The biofilm evolution equation (the rate at which the biofilm is moving in the vertical direction) is
\[\frac{dh}{dt} = h+ h_x^2.\]The biofilm will keep the same shape if \(\frac{dh}{dt}\) is a constant for all \(x\) since this implies that all points are moving at the same rate. This means we can take an x-derivative of the evolution equation and set it equal to zero. We are left with the differential equation:
\[0 = h_x(1+h_x^2+2hh_{xx}).\]We can solve this to see what the shape of the boundary is. We find that \(\frac{\partial h}{\partial x} = \pm \sqrt{c/h-1}\) Where \(c\) is a constant. Doing a Taylor expansion, this equation implies that for small \(h\), hence near a boundary, the slope of the function is \(\frac{\partial h}{\partial x} = \pm\sqrt{c/h}\). Thus the slope goes to infinity at a rate like \(\frac{1}{\sqrt{h}}\). Below is an image of what this shape will look like:
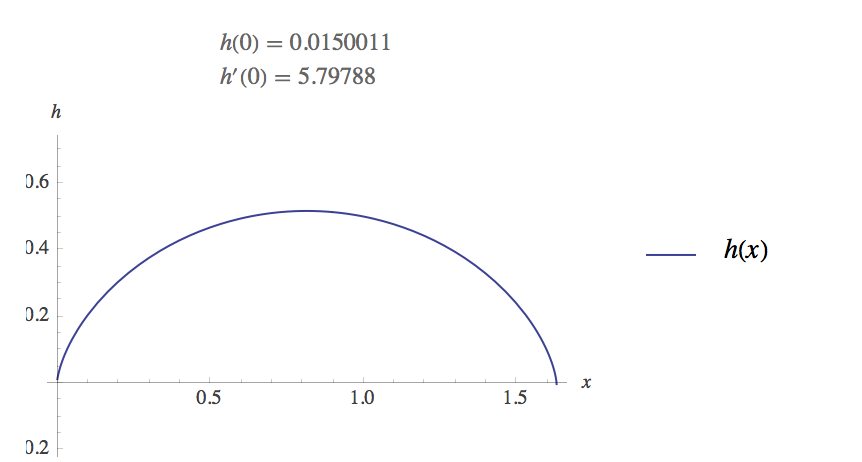
We would like to compare this predicted shape from the model to experimental data in order to validate the model.