I realized that there is an interesting problem with the formulation I have for the lateral expansion of biofilm in my model. I am using a functional representation of the biofilm interface and doing biofilm height and growth velocity extensions into regions of the domain where there is no biofilm layer. For more detail on this you can look at my previous post.

The problem I’m having is that the biofilm interface will get stuck and not spread to the rest of the domain. The problem is that for the interface to move outward together, we need the derivative at the boundary of the biofilm to go to infinity as the height goes to zero. However, in our simulation, the biofilm height is limited by the height of the channel and \(dx\) is fixed by the grid. This means that at most the computed derivative could be the height of the biofilm divided by \(dx\). Thus the derivative can’t go to infinity.

I performed a simulation where I tried to mitigate this problem by making \(dx\) really small, allowing for the height derivative to be large. There is some movement of the interface, particularly toward the inlet. But in order to have this movement the biofilm height next to the interface has to be extremely large. In reality the biofilm interface should be smooth and just limit to an infinite derivative at the boundary. Below is an image of the moving interface in time.

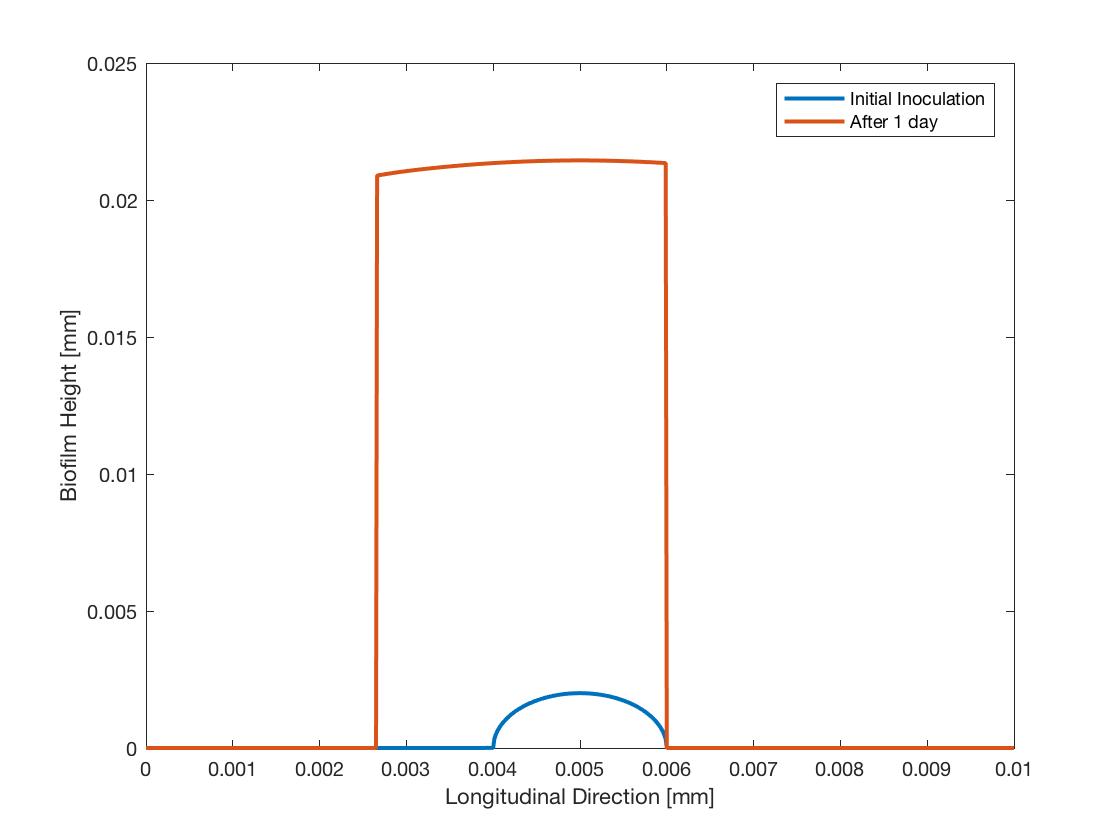
OutwardGrowth

I haven’t found a solution to this problem yet. It might be a problem in how we are calculating growth, but I think the problem is more basic. Maybe we can’t use a functional representation of the interface for this problem. I’m looking for solutions now, but they might entail using something like level set methods for the boundary.